哪吒D1的cache line是32字节还是64字节
另外,我看dcache是32KB,意思是这个只有L1cache,大小是32KB吗?
zhaodongyu 发布的最佳帖子
-
哪吒D1的cache line是多大发布在 MR Series
-
记录在D1上优化SGEMM(单精度浮点通用矩阵乘法)发布在 MR Series
几个月前在 D1 上搞过一段时间的 RISC-V,当时优化 SGEMM 期间经常在这个论坛提问,获得了很多帮助。本着互助精神,把之前的一些尝试在这里分享给大家,一起进步~
Github: https://github.com/Zhao-Dongyu/sgemm_riscv
欢迎star!【
 本文动图较多,将加载大约 40MB 图片资源,请耐心等待
本文动图较多,将加载大约 40MB 图片资源,请耐心等待  】
】
本项目记录了在riscv平台上优化SGEMM(单精度浮点通用矩阵乘法)的过程。
通用矩阵乘(
General Matrix Multiplication,简称gemm)是深度学习框架的核心计算单元之一,广泛用于Convolution、Full connection、Matmul等算子实现。我是在 全志 Nezha D1 开发板上进行的实验与探索,
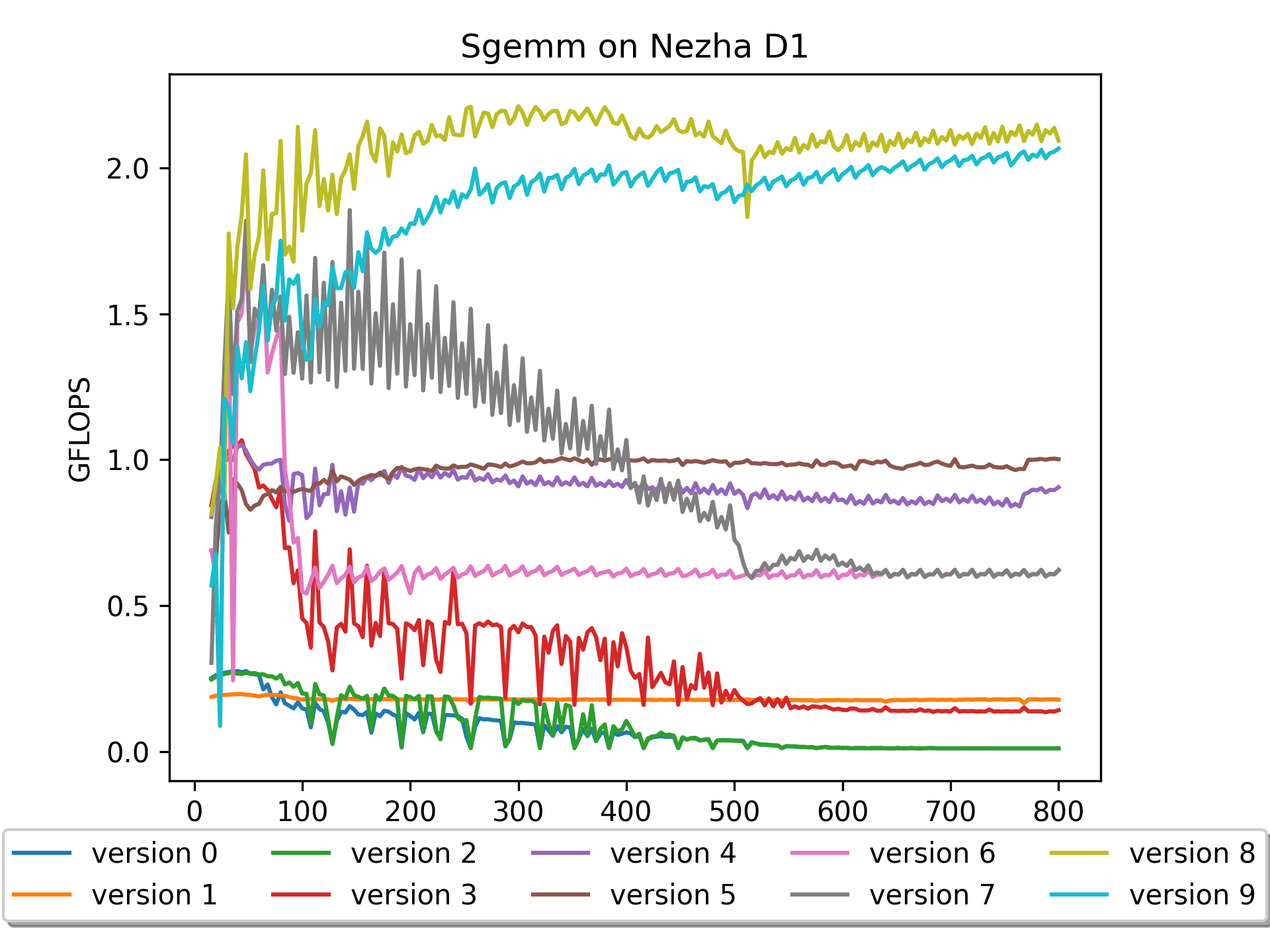
version 0 - version 5是使用的 C 语言,version 6 - version 9则部分使用了汇编,涉及到RISC-V V扩展指令。注意:不同于其他的某些gemm优化工程,在本工程中,全部使用 行主序 的矩阵。因为我喜欢 行主序!
预备知识

RISC-V 是一种开放标准指令集架构 (ISA),通过开放协作开启处理器创新的新时代。
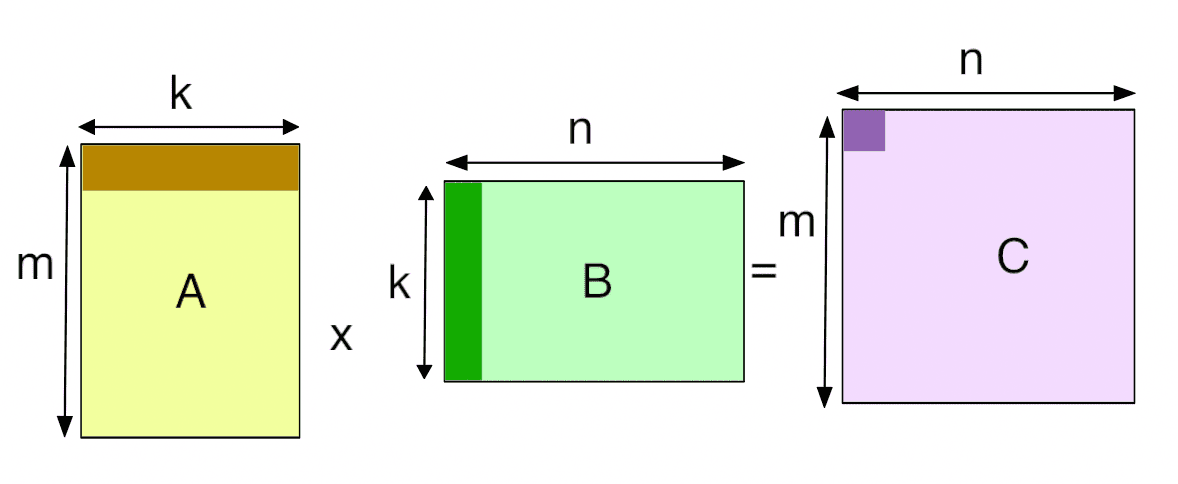
GEMM 通用矩阵乘法,基本线性代数子程序之一。
FLOPS每秒浮点运算次数,亦称每秒峰值速度,(英语:
Floating-point operations per second;缩写:FLOPS),即每秒所执行的浮点运算次数。一个GFLOPS(gigaFLOPS)等于每秒十亿(10^9)次的浮点运算;矩阵乘的计算量是
2 * M * N * K,计算量除以耗时即为当前gemm版本的gflops。- 乘以 2 是因为每次操作包含一次乘法和一次加法
准备工作
相关代码位于
./prepare/。测试交叉编译
我使用的 全志 Nezha D1 开发板,在这里下载的交叉编译链接。
详细教程见readme
内存带宽测试
分别通过以下几个小工程对开发板内存带宽进行测试

roofline模型
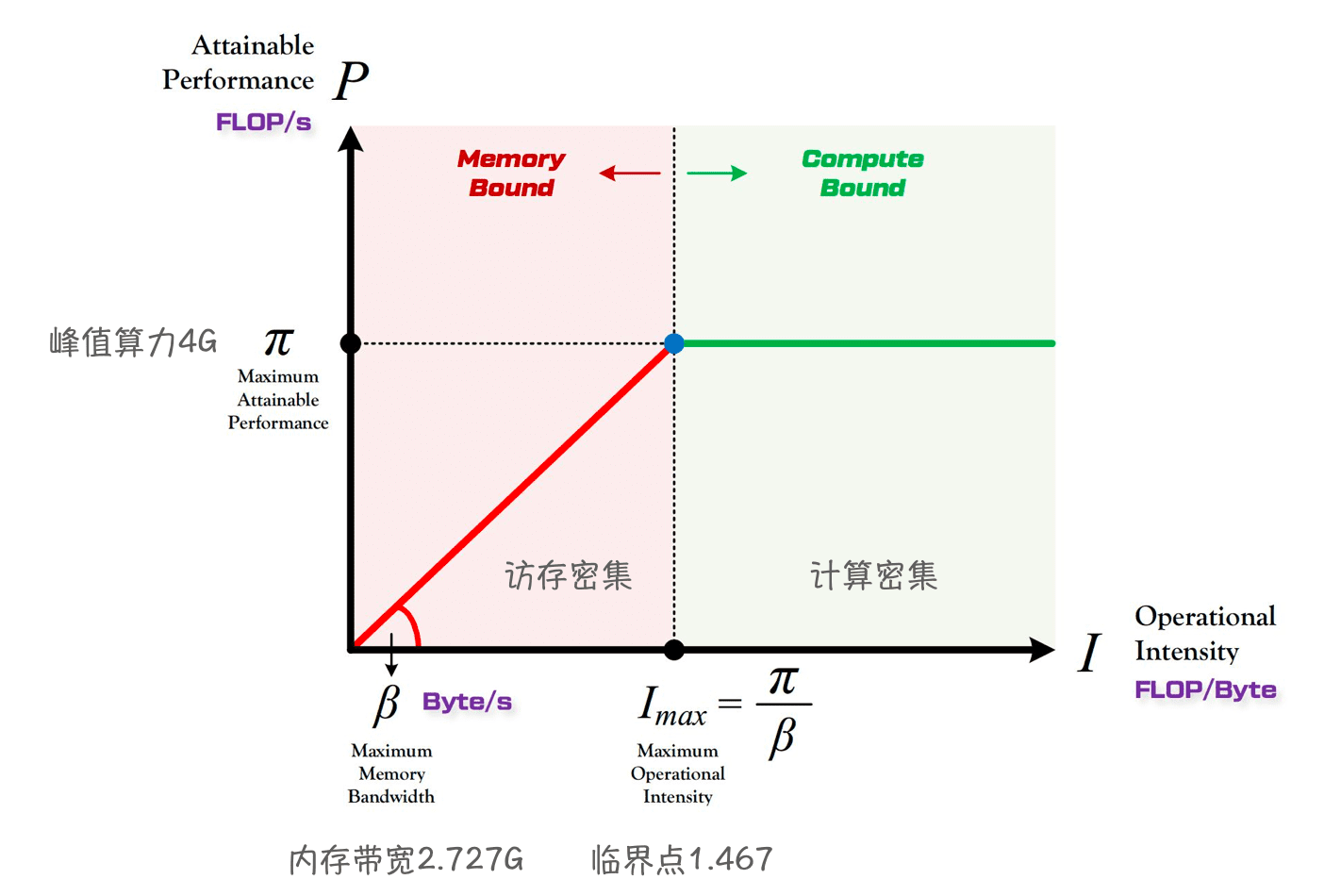
Roofline 提出了使用
Operational Intensity(计算强度)进行定量分析的方法,并给出了模型在计算平台上所能达到理论计算性能上限公式。D1的算力可达4 GFlops(@1GHz)- Memory :
2.727 GB/s(DDR3 792 MHz)。- 虽然我测出来最高是
2.592 GB/s,可能哪里出了问题? - 商汤还是要相信一下的,暂时以他的为准吧
- 虽然我测出来最高是
sgemm优化
相关代码位于
./sgemm/。使用说明
以
step0为例,你需要先编辑 Makefile ,配置自己的交叉编译链。$ cd sgemm/step0/ $ make $ adb push test_bl_sgemm_step0.x ./. $ adb shell './test_bl_sgemm_step0.x'Version 0: naive版本
这个版本思路在我看来是最直观的,毕竟我当时就是这么学习、理解和计算矩阵乘法的:
A 的一行乘以 B 的一列得到 C 的一个元素。

for ( i = 0; i < m; i ++ ) { // Start 2-th loop for ( j = 0; j < n; j ++ ) { // Start 1-nd loop for ( p = 0; p < k; p ++ ) { // Start 0-st loop C( i, j ) += A( i, p ) * B( p, j ); } // End 0-th loop } // End 1-st loop } // End 2-nd loop我认为
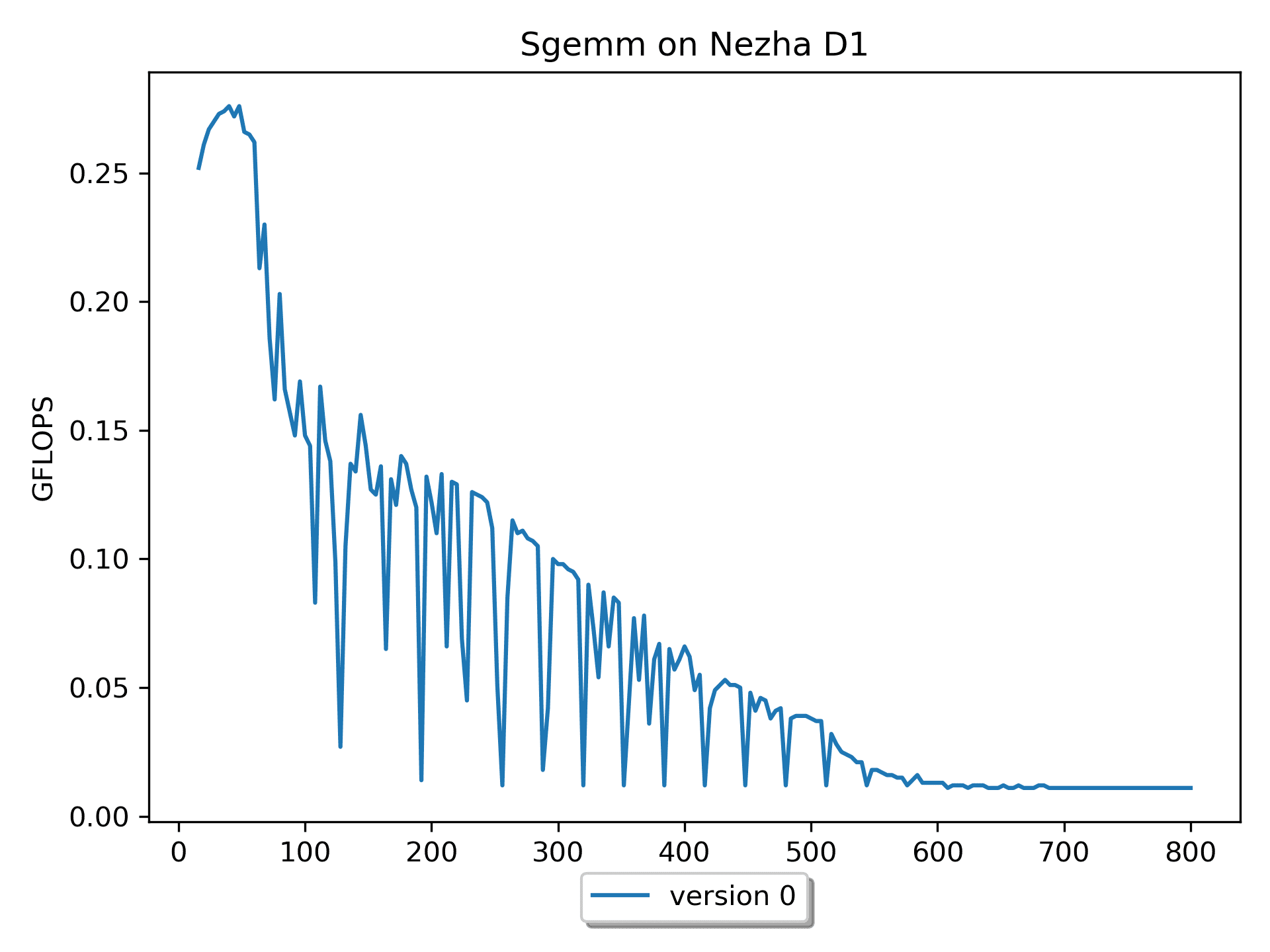
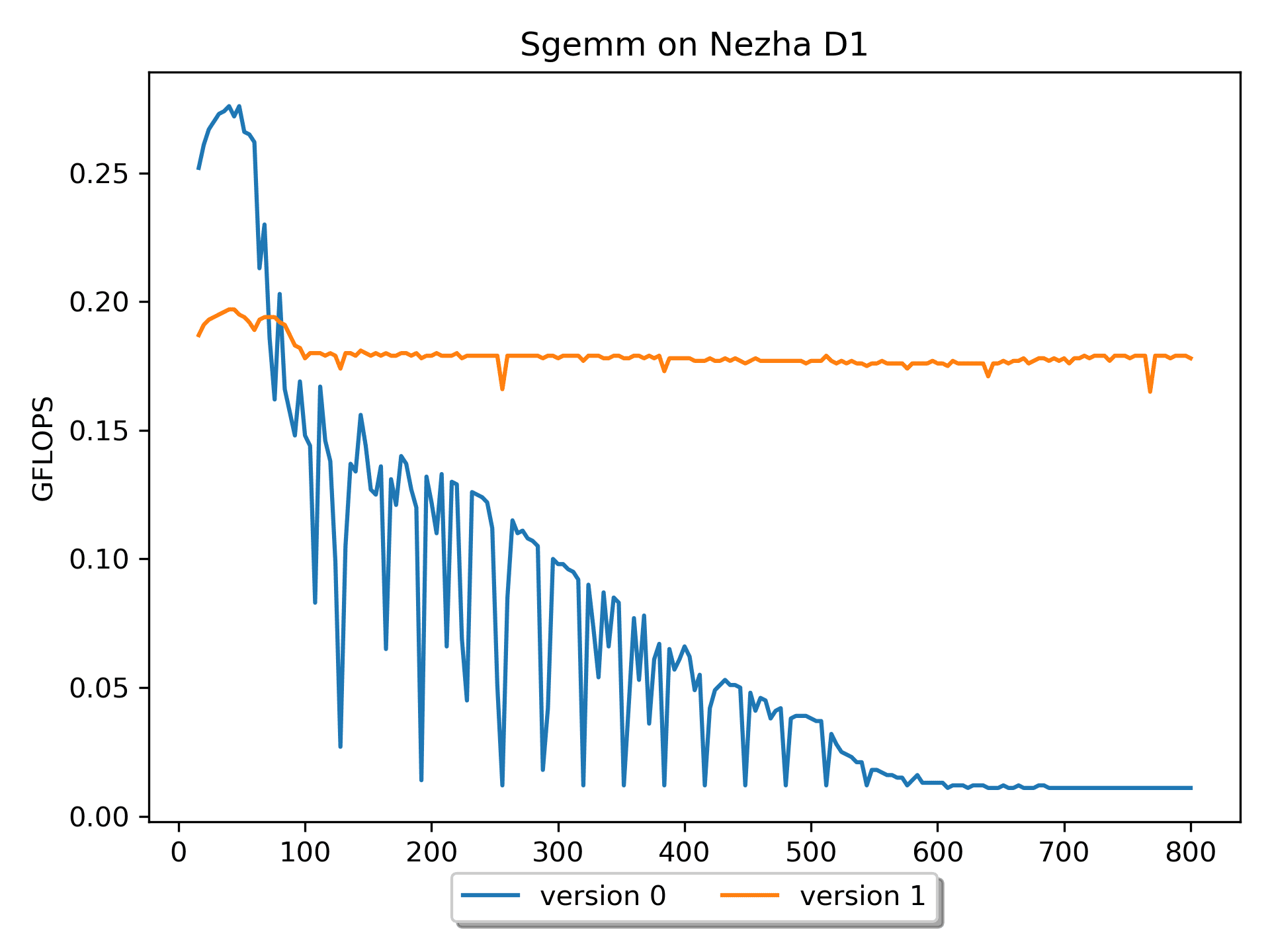
version 0非常契合的解释了 $C_{mn} = \sum_{k=1}^{K} A_{mk}B_{kn}$ 这个公式。但是这个版本缺点比较明显:在理论算力为
4 GFLOPS的平台仅发挥出最大0.03 GFLOPS的计算性能。这是因为对于矩阵B的访问,cache命中率极低,即「空间局部性很差」。整个计算下来,相当于访问矩阵B的次数多了很多很多次。对于多维数组的元素尽量能按照顺序访问。这样可以改善内存访问的空间局部性,对缓存更加友好。
另外,观察到随着尺寸的增加,性能有较大的抖动。分析数据可以知道:当
m=n=k为 128 164 192 228 256 288 320 352 384 时性能都很差。这几个数相差32,32 * 4(sizeof(float)) = 128 B。猜测性能抖动与
cacheline以及硬件预取有关—— cacheline = 64B,cache miss 后,硬件预取即HWPrefetcher,多读 1 个 cacheline。Version 1: 循环交换版本
重复使用Cache中的数据是最基本的高效使用Cache方法。对于多层嵌套循环,可以通过交换两个嵌套的循环(
loop interchange)、逆转循环迭代执行的顺序(loop reversal)、将两个循环体合并成一个循环体(loop fusion)、循环拆分(loop distribution)、循环分块(loop tiling)、loop unroll and jam等循环变换操作。选择适当的循环变换方式,既能保持程序的语义,又能改善程序性能。
for ( i = 0; i < m; i ++ ) { // Start 2-th loop for ( p = 0; p < k; p ++ ) { // Start 1-st loop for ( j = 0; j < n; j ++ ) { // Start 0-nd loop C( i, j ) += A( i, p ) * B( p, j ); } // End 0-th loop } // End 1-st loop } // End 2-nd loop相较于
version 0,version 1对于矩阵B的操作,空间局部性较好,性能有较大提升(尤其是对于尺寸较大的情况,而在 m = n = k <= 68 时,版本0的效率更高)。调整m,n,k的顺序,对结果没有影响(即保持程序的语义),但是可以影响性能。
测试不同循环顺序的性能(全志Nezha D1平台,以m=n=k=512为例)循环顺序 GFLOPS 分析 MNK 0.012 访问B的cache miss高 MKN 0.180 NMK 0.012 访问B的cache miss高 NKM 0.009 访问A的cache miss高 KMN 0.165 KNM 0.009 访问A的cache miss高 但是,
version 1的硬件使用率仍然很低,继续想办法优化。Version 2: 分块版本


for ( i = 0; i < m; i += DGEMM_MR ) { // Start 2-nd loop for ( j = 0; j < n; j += DGEMM_NR ) { // Start 1-st loop AddDot_4x4_opt( k, &A( i, 0 ), lda, &B( 0, j ), ldb, &C( i, j ), ldc ); } // End 1-st loop } // End 2-nd loop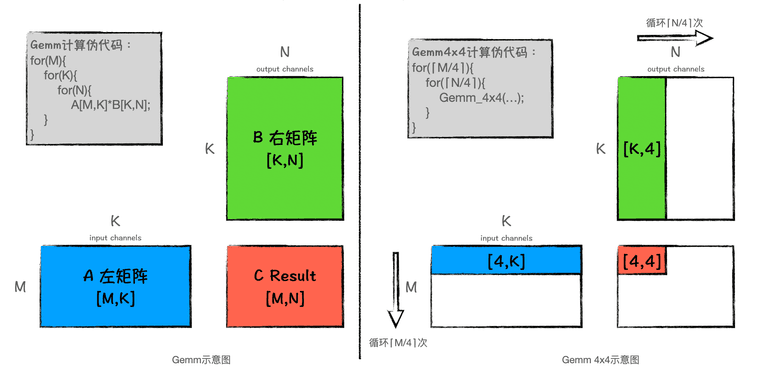
为了避免多余的 cache 换入换出,于是进行分块处理。浅谈分块矩阵优化方法为什么有用一文讲的挺好,建议阅读学习。
版本2进行了分块操作后,性能仍然不理想,这是因为,这个版本只是表面逻辑上实现了分块,块内的计算还有一些小技巧没有应用。
Version 3: 分块优化版本
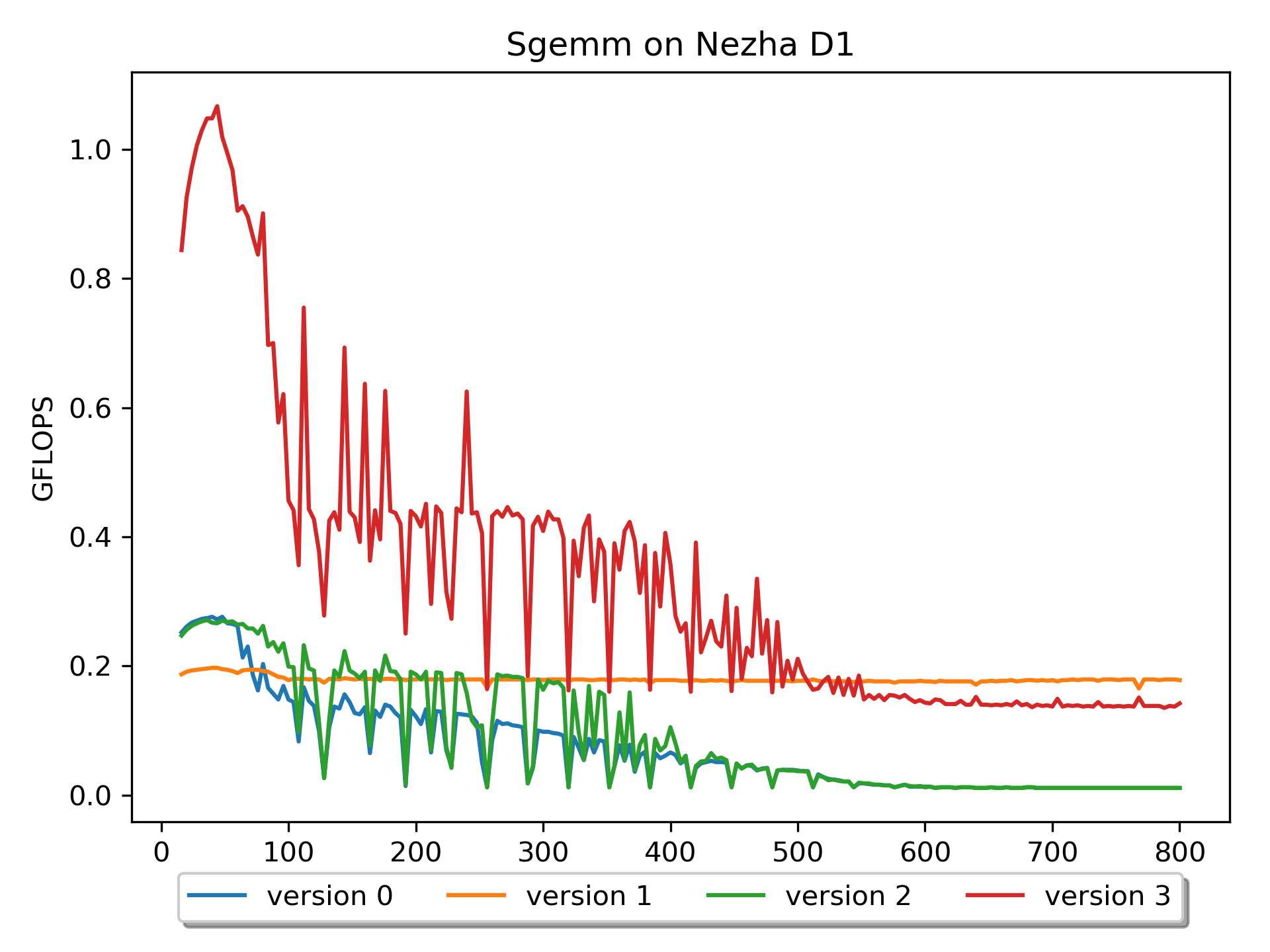
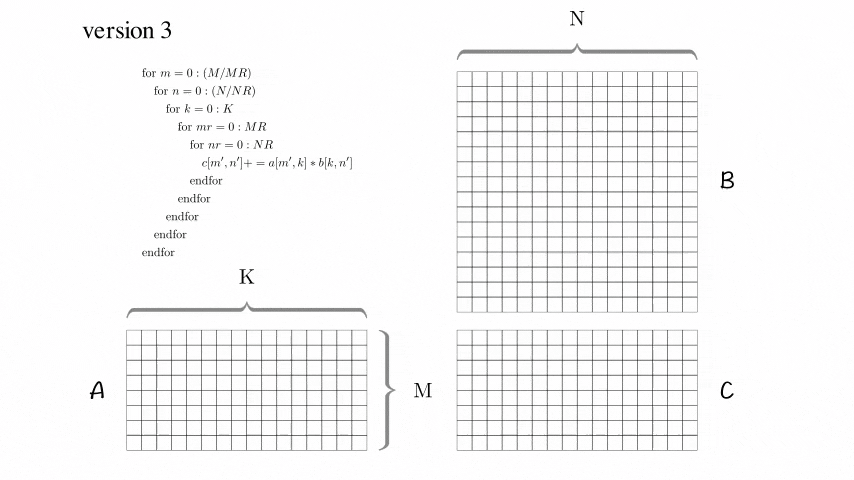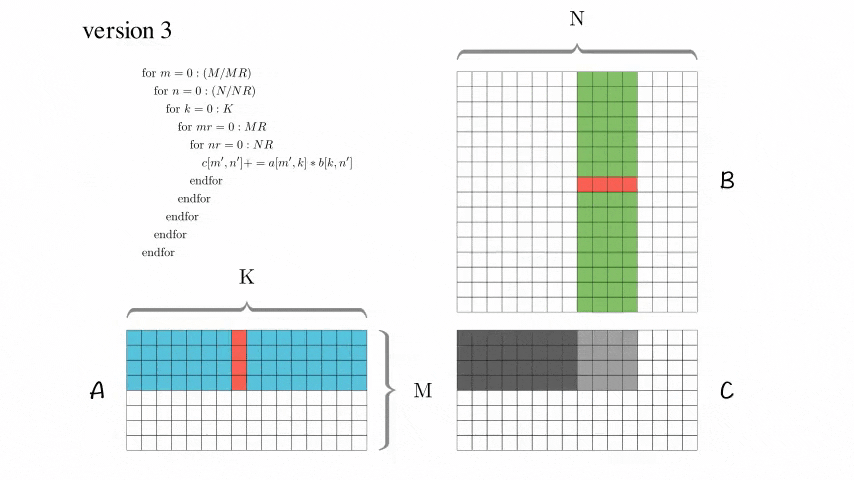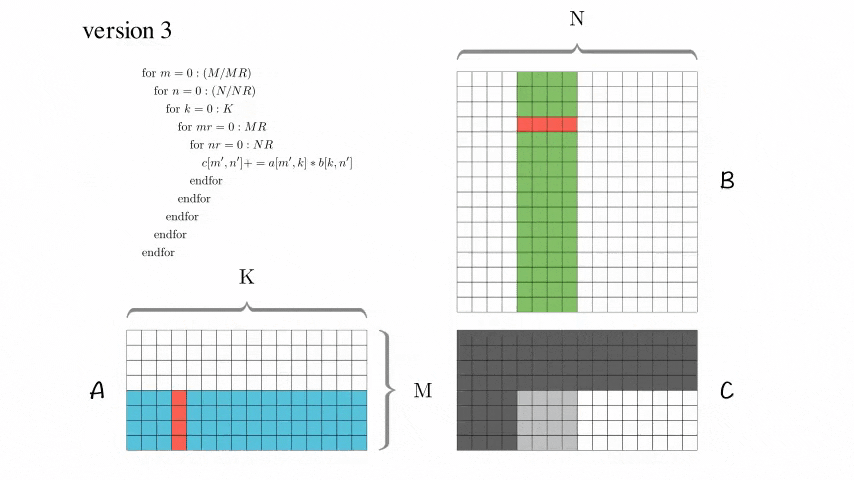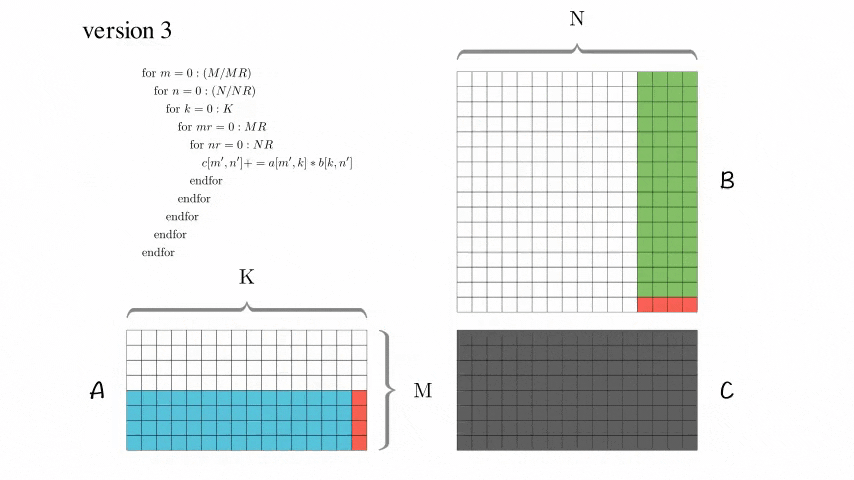
增加了AddDot_4x4_opt
在BLISlab-tutorial中提到了几个小技巧:
-
循环展开 2.4.2 Loop unrolling
- Updating loop index i and the pointer cp every time through the inner loop creates considerable overhead. For this reason, a compiler will perform loop unrolling.
-
寄存器缓存 2.4.3 Register variables
- Notice that computation can only happen if data is stored in registers. A compiler will automatically transform code so that the intermediate steps that place certain data in registers is inserted.
使用了这个技巧后,这个版本性能有了大幅度的提升!
然而,这个版本对于尺寸较大的矩阵,性能仍然比较低。查找原因,比如访问B[0,0], B[0,1], B[0,2], B[0,3]后,访问B[1,0]的时候,当尺寸较大的时候必定
cache miss。因此,如果能提前把数据重新排列就好了。Version 4: B prepack版本
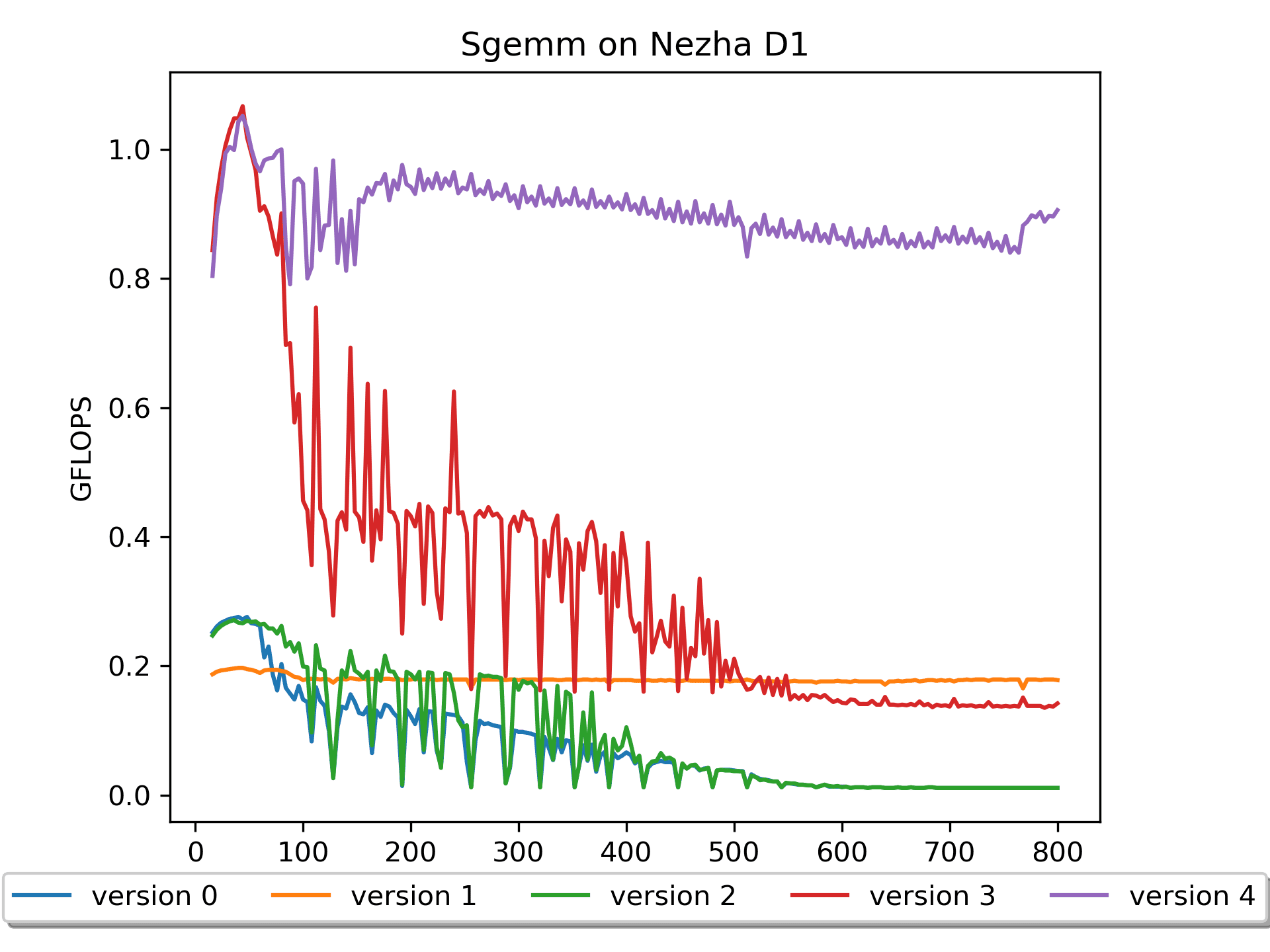

我默认矩阵B是参数,所以可以提前进行
pack操作。版本4对矩阵B进行了prepack,性能更进一步!性能提升的原因很明显:访问矩阵 B 的
cache miss明显减少了。这也是我第一次深刻意识到模型推理前对神经网络权重做prepack的重要性。可以看到,当尺寸比较大的时候,性能还是有所下降的。这应该是对矩阵A访问的
cache miss比较多。要对A做pack吗?我默认矩阵A是输入,因此对A做
pack的话是不能提前做的,是要算在整体时间内的。那么,有必要吗?Version 5: A pack & B prepack版本
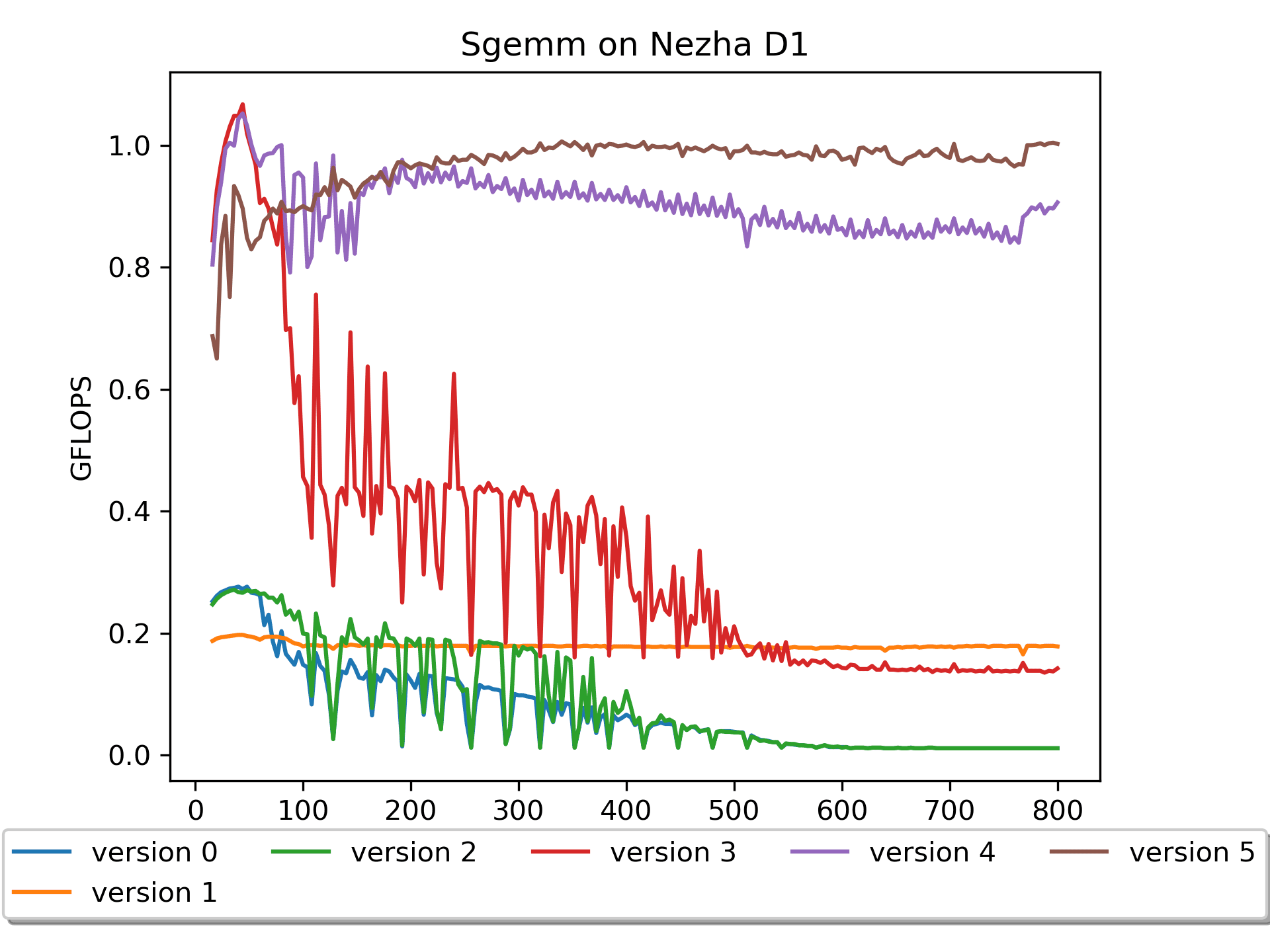
在版本4的基础上,版本5对矩阵A进行了
pack这里默认矩阵A是输入,所以需要在计算过程中进行
pack操作,这个耗时是要放在计时里面的。结果还是让人欣喜的,尤其是在大尺寸矩阵上,取得了进一步的性能提升。
我本来是试一试的心态做了这个尝试,毕竟这个操作会多读一遍
A以及写一遍packA。看来接下来主要就是与cache miss作斗争了。目前思路方面的优化基本到头了,在计算过程中做一些
preload是值得尝试一下的。接下来上汇编,搞向量计算,以及在汇编里面做
preload。Version 6: 汇编版本
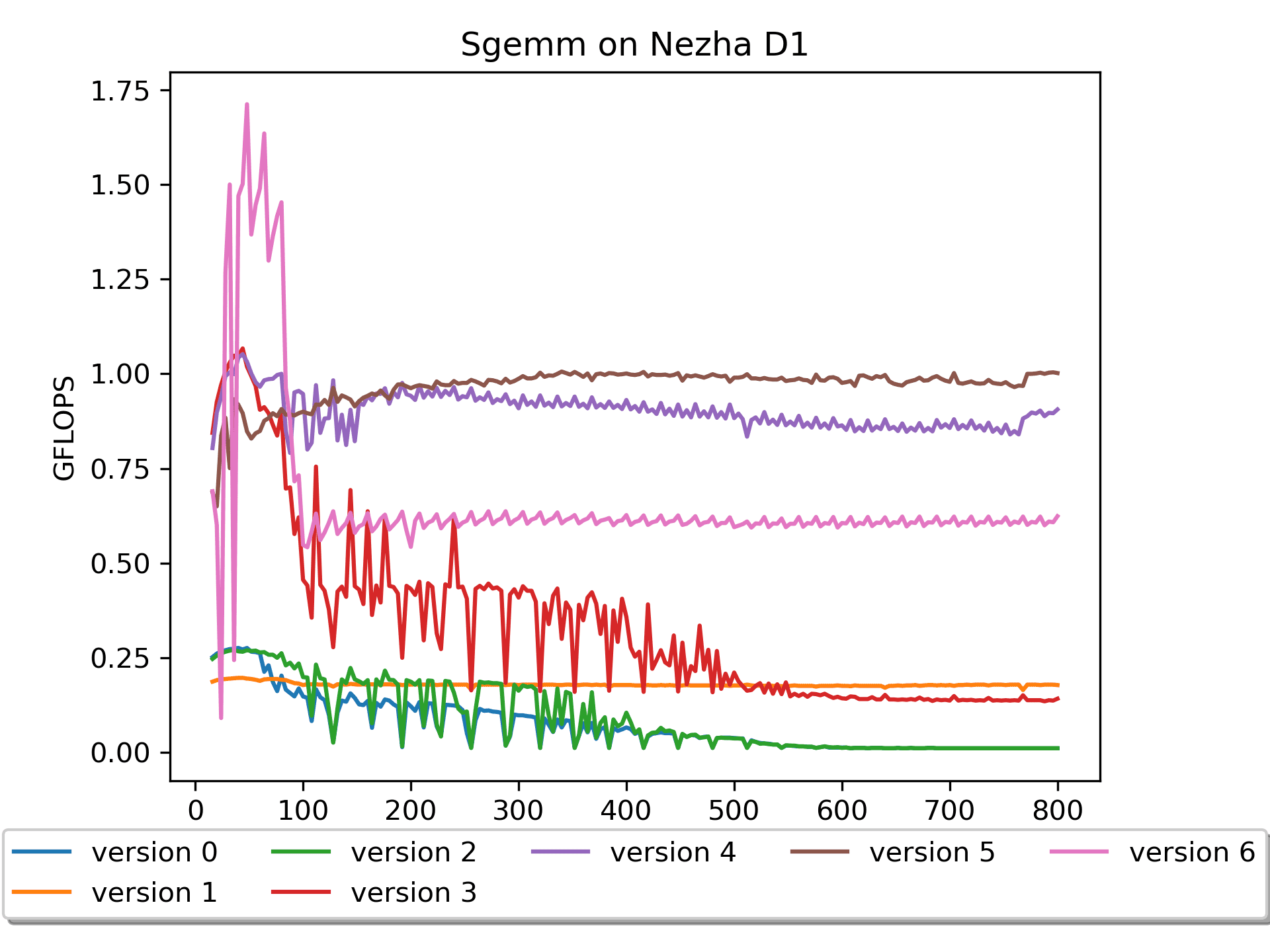
简要说明:A没有
pack,B进行了16个数的prepack。for ( i = 0; i < m; i += DGEMM_MR ) { // Start 2-nd loop int mb = DGEMM_MR; if((m - i) < DGEMM_MR) mb = m - i; for ( j = 0; j < n; j += DGEMM_NR ) { // Start 1-st loop int nb = DGEMM_NR; if((n - j) < DGEMM_NR) nb = n - j; RvvSgemm4x16( nb, // nr <= 16, a0 mb, // mr <= 4, a1 k, // astride = k*sizeof(float), a2 &A[i * k], // mr * k, a3 &packB[j * k], // k * 16, a4 &C( i, j ), // mr * nr, a5 n * sizeof(float), // Len(N) * sizeof(float), a6 bias ); } // End 1-st loop } // End 2-nd loop关于
rvv指令的使用,我认为vsetvli是灵魂,vfmacc.vf是主力。关于这些内容,我从OpenPPL 公开课 | RISC-V 技术解析学到了很多,他们可真专业啊!建议理论指导和知识点学习去他们那里学,向
OpenPPL致敬!至于汇编算子,汇编里面的小细节就多了,强烈吐槽:写汇编真烦人啊!尤其是 debug 过程,很折磨人。
我上次写汇编还是本科上课的时候,重新拾起还是有一些新奇和兴奋的,而且能够非常细粒度的控制算子执行,成就感还是很大的。关于汇编文件具体怎么实现的,我认为最快的方式就是去看汇编代码。这里就不多做解释了
需要注意的是,这个版本效果很差,这是为什么呢?又是 循环顺序 的问题。
Version 7: 汇编版本 调换循环顺序
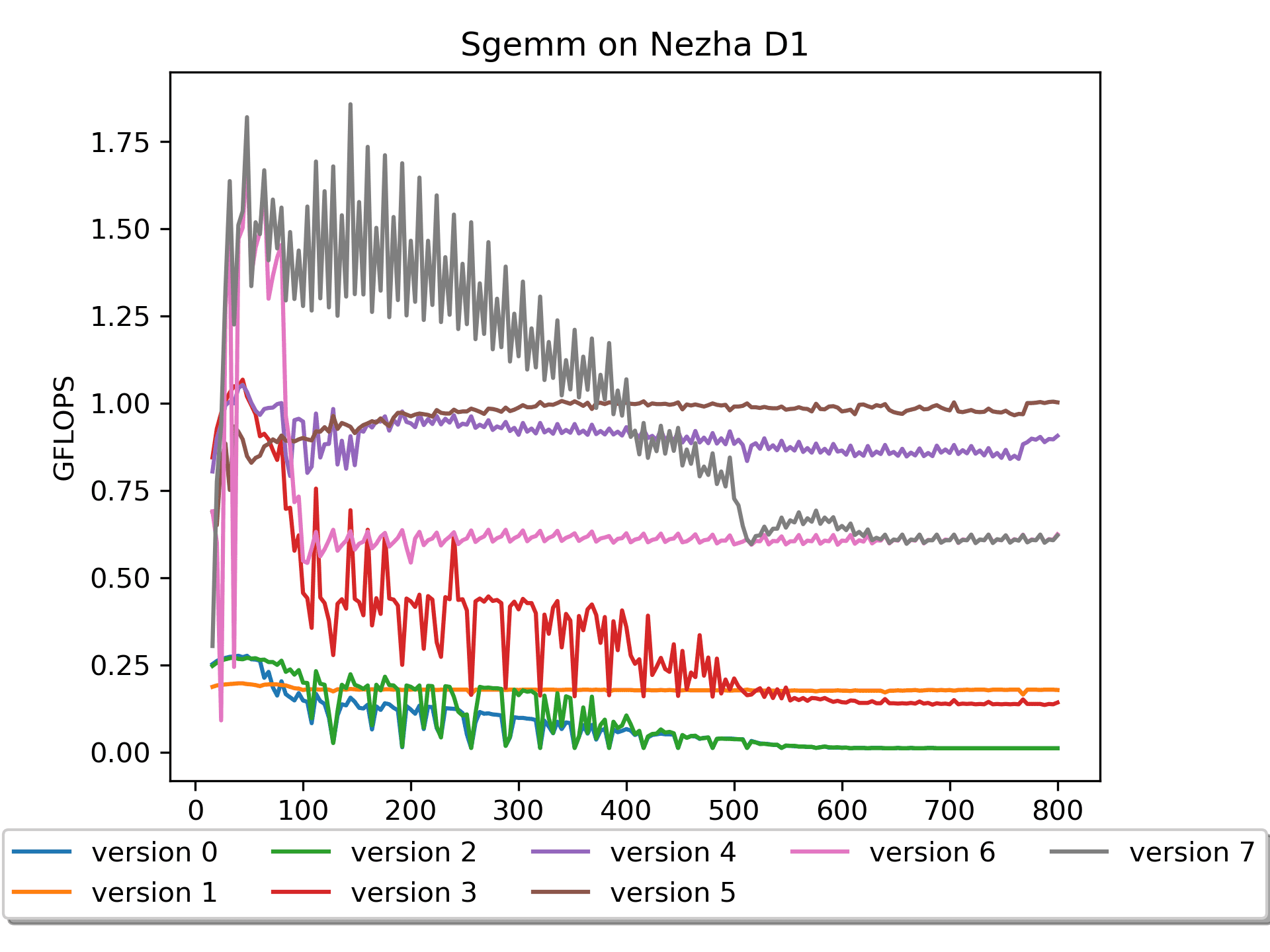
简要说明:A没有
pack,B进行了16个数的prepack。for ( j = 0; j < n; j += DGEMM_NR ) { // Start 2-st loop int nb = DGEMM_NR; if((n - j) < DGEMM_NR) nb = n - j; for ( i = 0; i < m; i += DGEMM_MR ) { // Start 1-nd loop int mb = DGEMM_MR; if((m - i) < DGEMM_MR) mb = m - i; RvvSgemm4x16( nb, // nr <= 16, a0 mb, // mr <= 4, a1 k, // astride = k*sizeof(float), a2 &A[i * k], // mr * k, a3 &packB[j * k], // k * 16, a4 &C( i, j ), // mr * nr, a5 n * sizeof(float), // Len(N) * sizeof(float), a6 bias ); } // End 1-st loop } // End 2-nd loop调换了循环的次序,先n方向后m方向,性能大大提升。
但是,大尺寸矩阵的性能还不是很好。究其原因,还是在访存上。大尺寸矩阵的计算在
roofline模型里属于是计算密集型,理想情况是计算的时间和访存的时间尽可能重叠,而现在基本是花很多时间在访存了(又是因为cache miss!)。Version 8: 汇编版本 加入preload
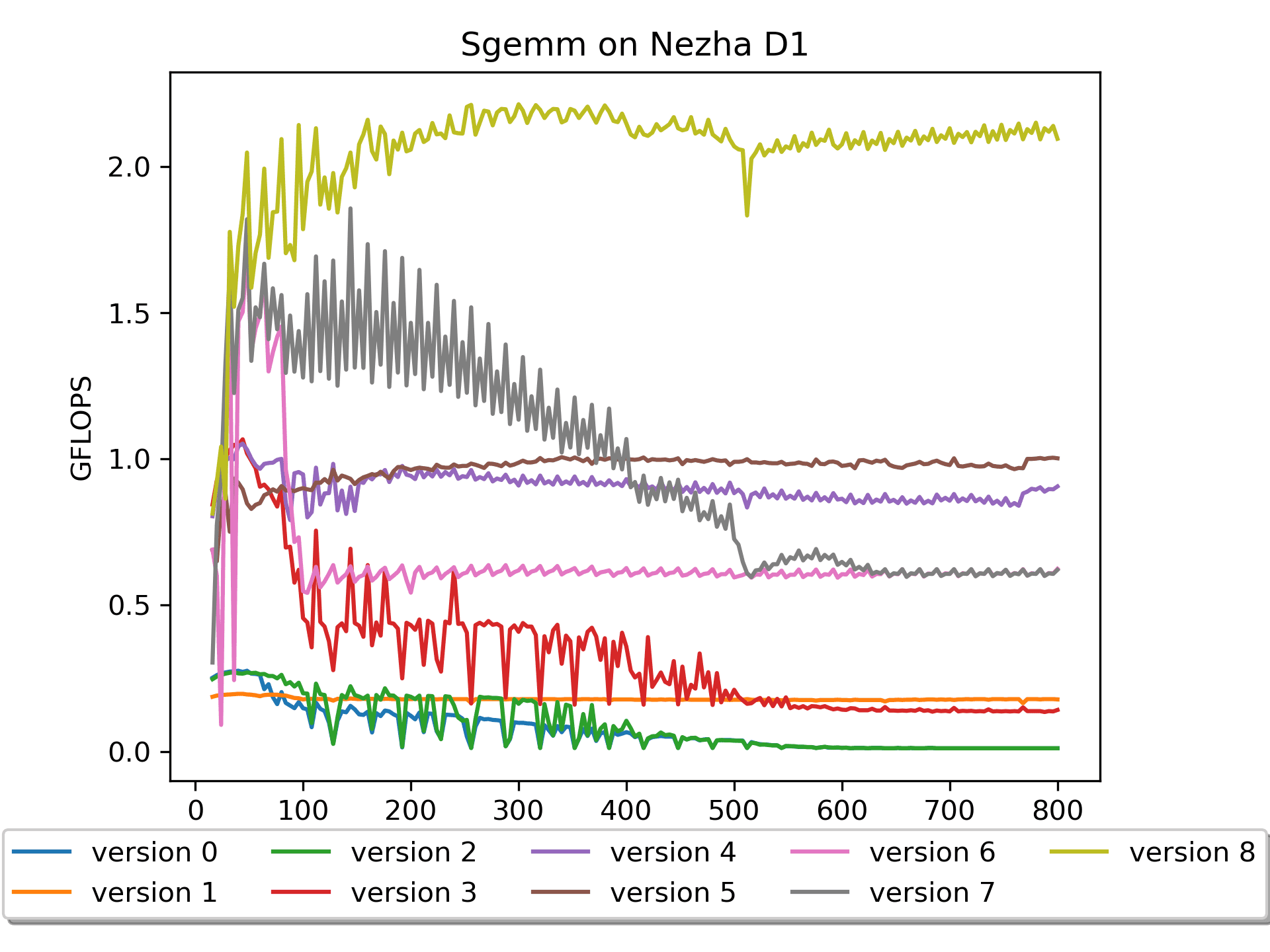
简要说明:A没有
pack,B进行了16个数的prepack,做了preload操作。性能相对爆炸!最高达到了
2.212 GFLOPS。核心操作:
vfmacc.vf v16, ft0, v0 vlw.v v4, (bp0) # b0'->v4 flw fs4, 384(bp0) # pre-load B addi bp0,bp0,64 vfmacc.vf v20, ft1, v0在
vfmacc.vf之间加入一些load操作,把之后要用到的数据提前load到cache中,可以大大降低cache miss。我最开始很疑惑——这样看代码明明也是顺序计算,怎么做到计算的时间和访存的时间重叠的呢?直到后来了解到
cacheline的原理才明白这里的精髓,果然基础知识很重要啊。Version 9: 汇编版本 A做pack
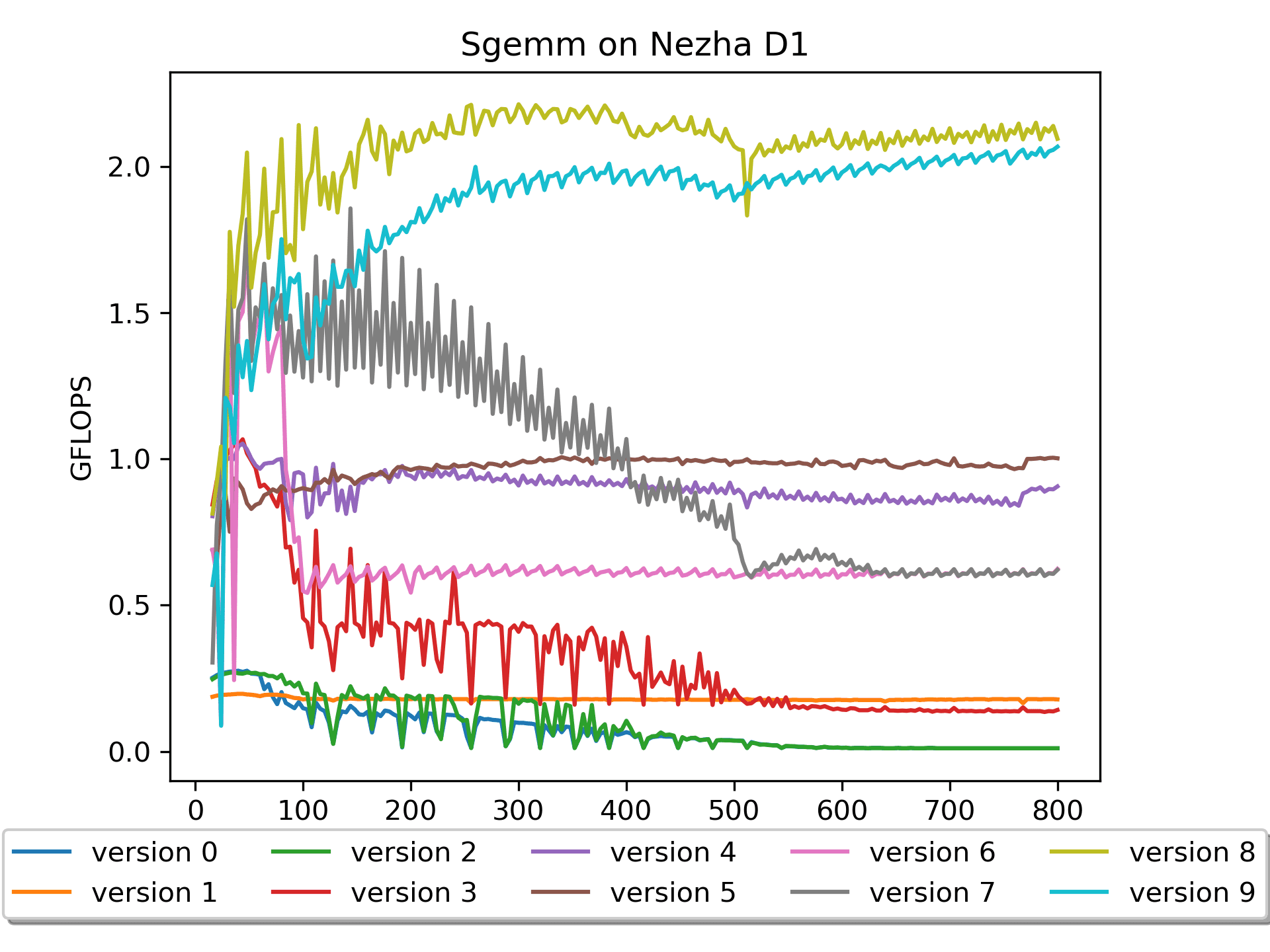
按照之前的经验,也尝试对 矩阵A 做了一下
pack,出乎意料的是结果不是很好。稍微分析了一下,应该是这个版本的汇编对 矩阵A 的preload写得不是很好。上个版本虽然对A没有pack,但是对4排的A都有
preload,所以也算是解决了矩阵A的cache miss的痛点吧。总结
要想继续优化这个算子,后续要做的事情还有很多,比如在汇编里面重排流水线。
在OpenPPL 公开课 | RISC-V 技术解析中也提到,如果使用 vf 指令,能够达到它理论峰值的 80%,即 4*80%,3.2GFLOPs。我现在只有
2.121 GFLOPS,理论上还是有很大优化空间的。另外, RVV目前用的是
0.7.1版本,感觉RVV的指令优化还是有很多工作要做,比如,目前遇到最严重的vlw效率低的问题。总之,做这些工作让我从很多大佬那里学到了很多知识,非常感谢。同时也希望本文能帮助到更多的人。
致谢
-
BLISlab: A Sandbox for Optimizing GEMM
这个项目让我了解了如何优化GEMM。
-
我基于这个项目进行了实验和探索。
-
感谢丁大佬的指导。
参考文章
zhaodongyu 发布的最新帖子
-
记录在D1上优化SGEMM(单精度浮点通用矩阵乘法)发布在 MR Series
几个月前在 D1 上搞过一段时间的 RISC-V,当时优化 SGEMM 期间经常在这个论坛提问,获得了很多帮助。本着互助精神,把之前的一些尝试在这里分享给大家,一起进步~
Github: https://github.com/Zhao-Dongyu/sgemm_riscv
欢迎star!【
 本文动图较多,将加载大约 40MB 图片资源,请耐心等待
本文动图较多,将加载大约 40MB 图片资源,请耐心等待  】
】
本项目记录了在riscv平台上优化SGEMM(单精度浮点通用矩阵乘法)的过程。
通用矩阵乘(
General Matrix Multiplication,简称gemm)是深度学习框架的核心计算单元之一,广泛用于Convolution、Full connection、Matmul等算子实现。我是在 全志 Nezha D1 开发板上进行的实验与探索,
version 0 - version 5是使用的 C 语言,version 6 - version 9则部分使用了汇编,涉及到RISC-V V扩展指令。注意:不同于其他的某些gemm优化工程,在本工程中,全部使用 行主序 的矩阵。因为我喜欢 行主序!
预备知识

RISC-V 是一种开放标准指令集架构 (ISA),通过开放协作开启处理器创新的新时代。

GEMM 通用矩阵乘法,基本线性代数子程序之一。
FLOPS每秒浮点运算次数,亦称每秒峰值速度,(英语:
Floating-point operations per second;缩写:FLOPS),即每秒所执行的浮点运算次数。一个GFLOPS(gigaFLOPS)等于每秒十亿(10^9)次的浮点运算;矩阵乘的计算量是
2 * M * N * K,计算量除以耗时即为当前gemm版本的gflops。- 乘以 2 是因为每次操作包含一次乘法和一次加法
准备工作
相关代码位于
./prepare/。测试交叉编译
我使用的 全志 Nezha D1 开发板,在这里下载的交叉编译链接。
详细教程见readme
内存带宽测试
分别通过以下几个小工程对开发板内存带宽进行测试

roofline模型
Roofline 提出了使用
Operational Intensity(计算强度)进行定量分析的方法,并给出了模型在计算平台上所能达到理论计算性能上限公式。D1的算力可达4 GFlops(@1GHz)- Memory :
2.727 GB/s(DDR3 792 MHz)。- 虽然我测出来最高是
2.592 GB/s,可能哪里出了问题? - 商汤还是要相信一下的,暂时以他的为准吧
- 虽然我测出来最高是

sgemm优化
相关代码位于
./sgemm/。使用说明
以
step0为例,你需要先编辑 Makefile ,配置自己的交叉编译链。$ cd sgemm/step0/ $ make $ adb push test_bl_sgemm_step0.x ./. $ adb shell './test_bl_sgemm_step0.x'Version 0: naive版本
这个版本思路在我看来是最直观的,毕竟我当时就是这么学习、理解和计算矩阵乘法的:
A 的一行乘以 B 的一列得到 C 的一个元素。


for ( i = 0; i < m; i ++ ) { // Start 2-th loop for ( j = 0; j < n; j ++ ) { // Start 1-nd loop for ( p = 0; p < k; p ++ ) { // Start 0-st loop C( i, j ) += A( i, p ) * B( p, j ); } // End 0-th loop } // End 1-st loop } // End 2-nd loop我认为
version 0非常契合的解释了 $C_{mn} = \sum_{k=1}^{K} A_{mk}B_{kn}$ 这个公式。但是这个版本缺点比较明显:在理论算力为
4 GFLOPS的平台仅发挥出最大0.03 GFLOPS的计算性能。这是因为对于矩阵B的访问,cache命中率极低,即「空间局部性很差」。整个计算下来,相当于访问矩阵B的次数多了很多很多次。对于多维数组的元素尽量能按照顺序访问。这样可以改善内存访问的空间局部性,对缓存更加友好。
另外,观察到随着尺寸的增加,性能有较大的抖动。分析数据可以知道:当
m=n=k为 128 164 192 228 256 288 320 352 384 时性能都很差。这几个数相差32,32 * 4(sizeof(float)) = 128 B。猜测性能抖动与
cacheline以及硬件预取有关—— cacheline = 64B,cache miss 后,硬件预取即HWPrefetcher,多读 1 个 cacheline。Version 1: 循环交换版本
重复使用Cache中的数据是最基本的高效使用Cache方法。对于多层嵌套循环,可以通过交换两个嵌套的循环(
loop interchange)、逆转循环迭代执行的顺序(loop reversal)、将两个循环体合并成一个循环体(loop fusion)、循环拆分(loop distribution)、循环分块(loop tiling)、loop unroll and jam等循环变换操作。选择适当的循环变换方式,既能保持程序的语义,又能改善程序性能。


for ( i = 0; i < m; i ++ ) { // Start 2-th loop for ( p = 0; p < k; p ++ ) { // Start 1-st loop for ( j = 0; j < n; j ++ ) { // Start 0-nd loop C( i, j ) += A( i, p ) * B( p, j ); } // End 0-th loop } // End 1-st loop } // End 2-nd loop相较于
version 0,version 1对于矩阵B的操作,空间局部性较好,性能有较大提升(尤其是对于尺寸较大的情况,而在 m = n = k <= 68 时,版本0的效率更高)。调整m,n,k的顺序,对结果没有影响(即保持程序的语义),但是可以影响性能。
测试不同循环顺序的性能(全志Nezha D1平台,以m=n=k=512为例)循环顺序 GFLOPS 分析 MNK 0.012 访问B的cache miss高 MKN 0.180 NMK 0.012 访问B的cache miss高 NKM 0.009 访问A的cache miss高 KMN 0.165 KNM 0.009 访问A的cache miss高 但是,
version 1的硬件使用率仍然很低,继续想办法优化。Version 2: 分块版本


for ( i = 0; i < m; i += DGEMM_MR ) { // Start 2-nd loop for ( j = 0; j < n; j += DGEMM_NR ) { // Start 1-st loop AddDot_4x4_opt( k, &A( i, 0 ), lda, &B( 0, j ), ldb, &C( i, j ), ldc ); } // End 1-st loop } // End 2-nd loop
为了避免多余的 cache 换入换出,于是进行分块处理。浅谈分块矩阵优化方法为什么有用一文讲的挺好,建议阅读学习。
版本2进行了分块操作后,性能仍然不理想,这是因为,这个版本只是表面逻辑上实现了分块,块内的计算还有一些小技巧没有应用。
Version 3: 分块优化版本


增加了AddDot_4x4_opt
在BLISlab-tutorial中提到了几个小技巧:
-
循环展开 2.4.2 Loop unrolling
- Updating loop index i and the pointer cp every time through the inner loop creates considerable overhead. For this reason, a compiler will perform loop unrolling.
-
寄存器缓存 2.4.3 Register variables
- Notice that computation can only happen if data is stored in registers. A compiler will automatically transform code so that the intermediate steps that place certain data in registers is inserted.
使用了这个技巧后,这个版本性能有了大幅度的提升!
然而,这个版本对于尺寸较大的矩阵,性能仍然比较低。查找原因,比如访问B[0,0], B[0,1], B[0,2], B[0,3]后,访问B[1,0]的时候,当尺寸较大的时候必定
cache miss。因此,如果能提前把数据重新排列就好了。Version 4: B prepack版本


我默认矩阵B是参数,所以可以提前进行
pack操作。版本4对矩阵B进行了prepack,性能更进一步!性能提升的原因很明显:访问矩阵 B 的
cache miss明显减少了。这也是我第一次深刻意识到模型推理前对神经网络权重做prepack的重要性。可以看到,当尺寸比较大的时候,性能还是有所下降的。这应该是对矩阵A访问的
cache miss比较多。要对A做pack吗?我默认矩阵A是输入,因此对A做
pack的话是不能提前做的,是要算在整体时间内的。那么,有必要吗?Version 5: A pack & B prepack版本


在版本4的基础上,版本5对矩阵A进行了
pack这里默认矩阵A是输入,所以需要在计算过程中进行
pack操作,这个耗时是要放在计时里面的。结果还是让人欣喜的,尤其是在大尺寸矩阵上,取得了进一步的性能提升。
我本来是试一试的心态做了这个尝试,毕竟这个操作会多读一遍
A以及写一遍packA。看来接下来主要就是与cache miss作斗争了。目前思路方面的优化基本到头了,在计算过程中做一些
preload是值得尝试一下的。接下来上汇编,搞向量计算,以及在汇编里面做
preload。Version 6: 汇编版本

简要说明:A没有
pack,B进行了16个数的prepack。for ( i = 0; i < m; i += DGEMM_MR ) { // Start 2-nd loop int mb = DGEMM_MR; if((m - i) < DGEMM_MR) mb = m - i; for ( j = 0; j < n; j += DGEMM_NR ) { // Start 1-st loop int nb = DGEMM_NR; if((n - j) < DGEMM_NR) nb = n - j; RvvSgemm4x16( nb, // nr <= 16, a0 mb, // mr <= 4, a1 k, // astride = k*sizeof(float), a2 &A[i * k], // mr * k, a3 &packB[j * k], // k * 16, a4 &C( i, j ), // mr * nr, a5 n * sizeof(float), // Len(N) * sizeof(float), a6 bias ); } // End 1-st loop } // End 2-nd loop关于
rvv指令的使用,我认为vsetvli是灵魂,vfmacc.vf是主力。关于这些内容,我从OpenPPL 公开课 | RISC-V 技术解析学到了很多,他们可真专业啊!建议理论指导和知识点学习去他们那里学,向
OpenPPL致敬!至于汇编算子,汇编里面的小细节就多了,强烈吐槽:写汇编真烦人啊!尤其是 debug 过程,很折磨人。
我上次写汇编还是本科上课的时候,重新拾起还是有一些新奇和兴奋的,而且能够非常细粒度的控制算子执行,成就感还是很大的。关于汇编文件具体怎么实现的,我认为最快的方式就是去看汇编代码。这里就不多做解释了
需要注意的是,这个版本效果很差,这是为什么呢?又是 循环顺序 的问题。
Version 7: 汇编版本 调换循环顺序

简要说明:A没有
pack,B进行了16个数的prepack。for ( j = 0; j < n; j += DGEMM_NR ) { // Start 2-st loop int nb = DGEMM_NR; if((n - j) < DGEMM_NR) nb = n - j; for ( i = 0; i < m; i += DGEMM_MR ) { // Start 1-nd loop int mb = DGEMM_MR; if((m - i) < DGEMM_MR) mb = m - i; RvvSgemm4x16( nb, // nr <= 16, a0 mb, // mr <= 4, a1 k, // astride = k*sizeof(float), a2 &A[i * k], // mr * k, a3 &packB[j * k], // k * 16, a4 &C( i, j ), // mr * nr, a5 n * sizeof(float), // Len(N) * sizeof(float), a6 bias ); } // End 1-st loop } // End 2-nd loop调换了循环的次序,先n方向后m方向,性能大大提升。
但是,大尺寸矩阵的性能还不是很好。究其原因,还是在访存上。大尺寸矩阵的计算在
roofline模型里属于是计算密集型,理想情况是计算的时间和访存的时间尽可能重叠,而现在基本是花很多时间在访存了(又是因为cache miss!)。Version 8: 汇编版本 加入preload

简要说明:A没有
pack,B进行了16个数的prepack,做了preload操作。性能相对爆炸!最高达到了
2.212 GFLOPS。核心操作:
vfmacc.vf v16, ft0, v0 vlw.v v4, (bp0) # b0'->v4 flw fs4, 384(bp0) # pre-load B addi bp0,bp0,64 vfmacc.vf v20, ft1, v0在
vfmacc.vf之间加入一些load操作,把之后要用到的数据提前load到cache中,可以大大降低cache miss。我最开始很疑惑——这样看代码明明也是顺序计算,怎么做到计算的时间和访存的时间重叠的呢?直到后来了解到
cacheline的原理才明白这里的精髓,果然基础知识很重要啊。Version 9: 汇编版本 A做pack

按照之前的经验,也尝试对 矩阵A 做了一下
pack,出乎意料的是结果不是很好。稍微分析了一下,应该是这个版本的汇编对 矩阵A 的preload写得不是很好。上个版本虽然对A没有pack,但是对4排的A都有
preload,所以也算是解决了矩阵A的cache miss的痛点吧。总结
要想继续优化这个算子,后续要做的事情还有很多,比如在汇编里面重排流水线。
在OpenPPL 公开课 | RISC-V 技术解析中也提到,如果使用 vf 指令,能够达到它理论峰值的 80%,即 4*80%,3.2GFLOPs。我现在只有
2.121 GFLOPS,理论上还是有很大优化空间的。另外, RVV目前用的是
0.7.1版本,感觉RVV的指令优化还是有很多工作要做,比如,目前遇到最严重的vlw效率低的问题。总之,做这些工作让我从很多大佬那里学到了很多知识,非常感谢。同时也希望本文能帮助到更多的人。
致谢
-
BLISlab: A Sandbox for Optimizing GEMM
这个项目让我了解了如何优化GEMM。
-
我基于这个项目进行了实验和探索。
-
感谢丁大佬的指导。
参考文章
-
哪吒D1的cache line是多大发布在 MR Series
哪吒D1的cache line是32字节还是64字节
另外,我看dcache是32KB,意思是这个只有L1cache,大小是32KB吗? -
RISCV支持的编译链发布在 MR Series
在论坛里看到
用最新的工具链,支持 rvv 1.0 intrinsics想问一下,这是真的支持了1.0指令集,还是做了一个0.7.1到1.0的映射?
我用的哪吒D1,想开发汇编的话要用0.7.1吗?为什么是0.7.1呢?(看大家都在说0.7.1)
1.0支持汇编调用1.0指令吗?还是只支持intrinsic的形式?
-
哪吒D1的内存带宽发布在 MR Series
不懂就问:
已知:DDR3 792 MHz
OpenPPL在https://zhuanlan.zhihu.com/p/474684731提到访存带宽是2.727 GB/s ;
我自测,用memcpy测的话,数据传输速度能达到是2.028GB/s;
单独用flw指令测试,结果是2.592GB/s。问:DDR3是792 MHz,访存带宽和它是什么关系呢?
问:OpenPPL的2.727GB/s是怎么测出来的?我实验vlw的速度比flw指令是慢的,难道还有比flw更快的指令? -
回复: 求证:riscv的计算与访存无法并行吗?发布在 MR Series
@aozima 多谢解答,另外想再问一下,计算和访存不能并行,这个意思是计算和访存不能双发射,但是他们有各自的流水线对吧?
