【跑个算法】之模拟退火算法在D1的执行

Randolph LV 6

前言：之前有做过一个VLSI布局布线相关的课题，学了一点关于模拟退火算法的毛皮，今天来跑个demo复（shui）习（tie）一下。

Simulated annealing这种算法的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由以下三部分组成：

（1）加温过程

（2）等温过程

（3）冷却过程

其中加温过程对应算法设定的初始温度，等温过程对应算法的Metropolis（一种采样算法）抽样过程，冷却过程对应控制参数的下降。这里能量的变化就是目标函数，要得到的最优解就是能量最低状态。Metropolis准则是SA算法收敛于全局最优解的关键所在，Metropolis准则以一定的概率接受恶化解。

总的来说就一句话：相比于类似爬山算法这种贪心算法，SA可以跳出局部最优解。

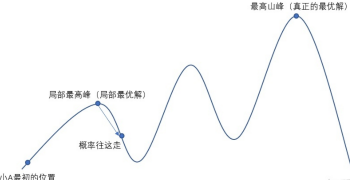
理解的大概原理后，就来看看代码。

/*
 * 使用模拟退火算法(SA)求解TSP问题(以中国TSP问题为例)
 * 参考自《Matlab 智能算法30个案例分析》
 * 模拟退火的原理这里略去，可以参考上书或者相关论文
 * update: 16/12/11
 * author:lyrichu
 * email:919987476@qq.com
 */
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<math.h>
#define T0 50000.0  // 初始温度
#define T_end (1e-8)
#define q  0.98   // 退火系数
#define L 1000  // 每个温度时的迭代次数，即链长
#define N 31  // 城市数量
int city_list[N]; // 用于存放一个解
double city_pos[N][2] = {{1304,2312},{3639,1315},{4177,2244},{3712,1399},{3488,1535},{3326,1556},{3238,1229},{4196,1004},{4312,790},
    {4386,570},{3007,1970},{2562,1756},{2788,1491},{2381,1676},{1332,695},{3715,1678},{3918,2179},{4061,2370},{3780,2212},{3676,2578},{4029,2838},
    {4263,2931},{3429,1908},{3507,2367},{3394,2643},{3439,3201},{2935,3240},{3140,3550},{2545,2357},{2778,2826},{2370,2975}}; // 中国31个城市坐标
//函数声明
double distance(double *,double *); // 计算两个城市距离
double path_len(int *);  // 计算路径长度
void  init();  //初始化函数
void create_new(); // 产生新解
// 距离函数
double distance(double * city1,double * city2)
{
    double x1 = *city1;
    double y1 = *(city1+1);
    double x2 = *(city2);
    double y2 = *(city2+1);
    double dis = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
    return dis;
}

// 计算路径长度
double path_len(int * arr)
{
    double path = 0; // 初始化路径长度
    int index = *arr; // 定位到第一个数字(城市序号)
    for(int i=0;i<N-1;i++)
    {
        int index1 = *(arr+i);
        int index2 = *(arr+i+1);
        double dis = distance(city_pos[index1-1],city_pos[index2-1]);
        path += dis;
    }
    int last_index = *(arr+N-1); // 最后一个城市序号
    int first_index = *arr; // 第一个城市序号
    double last_dis = distance(city_pos[last_index-1],city_pos[first_index-1]);
    path = path + last_dis;
    return path; // 返回总的路径长度
}

// 初始化函数
void init()
{
    for(int i=0;i<N;i++)
        city_list[i] = i+1;  // 初始化一个解
}

// 产生一个新解
// 此处采用随机交叉两个位置的方式产生新的解
void create_new()
{
    double r1 = ((double)rand())/(RAND_MAX+1.0);
    double r2 = ((double)rand())/(RAND_MAX+1.0);
    int pos1 = (int)(N*r1); //第一个交叉点的位置
    int pos2 = (int)(N*r2);
    int temp = city_list[pos1];
    city_list[pos1] = city_list[pos2];
    city_list[pos2] = temp;   // 交换两个点
}

// 主函数
int main(void)
{
    srand((unsigned)time(NULL)); //初始化随机数种子
    time_t start,finish;
    start = clock(); // 程序运行开始计时
    double T;
    int count = 0; // 记录降温次数
    T = T0; //初始温度
    init(); //初始化一个解
    int city_list_copy[N]; // 用于保存原始解
    double f1,f2,df; //f1为初始解目标函数值，f2为新解目标函数值，df为二者差值
    double r; // 0-1之间的随机数，用来决定是否接受新解
    while(T > T_end) // 当温度低于结束温度时，退火结束
    {
        for(int i=0;i<L;i++)
        {
            memcpy(city_list_copy,city_list,N*sizeof(int)); // 复制数组
            create_new(); // 产生新解
            f1 = path_len(city_list_copy);
            f2 = path_len(city_list);
            df = f2 - f1;
            // 以下是Metropolis准则
            if(df >= 0)
            {
                r = ((double)rand())/(RAND_MAX);
                if(exp(-df/T) <= r) // 保留原来的解
                {
                    memcpy(city_list,city_list_copy,N*sizeof(int));
                }
            }
        }
        T *= q; // 降温
        count++;
    }
    finish = clock(); // 退火过程结束
    double duration = ((double)(finish-start))/CLOCKS_PER_SEC; // 计算时间
    printf("采用模拟退火算法，初始温度T0=%.2f,降温系数q=%.2f,每个温度迭代%d次,共降温%d次，得到的TSP最优路径为:\n",T0,q,L,count);
    for(int i=0;i<N-1;i++)  // 输出最优路径
    {
        printf("%d--->",city_list[i]);
    }
    printf("%d\n",city_list[N-1]);
    double len = path_len(city_list); // 最优路径长度
    printf("最优路径长度为:%lf\n",len);
    printf("程序运行耗时:%lf秒.\n",duration);
    return 0;
}

这是网上找到一个商旅问题的SA解决方法例子，稍加修改后交叉编译一下到开发板上执行。

保存为test.c文件到哪吒SDK下后，执行：

$/prebuilt/gcc/linux-x86/riscv/toolchain-thead-glibc/riscv64-glibc-gcc-thead_20200702/bin/riscv64-unknown-linux-gnu-gcc -o test -lm test.c

用adb传送生成的可执行文件到开发板上，执行：

$chmod +x test
$./test

即可，下面看看执行效果：

D1s麻雀：

root@TinaLinux:/# ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
22--->18--->3--->17--->19--->16--->4--->2--->8--->9--->10--->7--->6--->5--->23--->11--->13--->12--->14--->15--->1--->29--->31--->30--->27--->28--->26--->25--->24--->20--->21
最优路径长度为:15385.425778
程序运行耗时:17.578781秒.
root@TinaLinux:/# ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
5--->6--->7--->10--->9--->8--->2--->4--->16--->19--->17--->3--->18--->22--->21--->20--->24--->25--->26--->28--->27--->30--->31--->29--->1--->15--->14--->12--->13--->11--->23
最优路径长度为:15385.425778
程序运行耗时:17.594397秒.
root@TinaLinux:/# ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
14--->15--->1--->29--->31--->30--->27--->28--->26--->25--->23--->4--->8--->9--->10--->2--->7--->6--->5--->16--->19--->17--->3--->18--->22--->21--->20--->24--->11--->13--->12
最优路径长度为:16245.867392
程序运行耗时:17.584901秒.

D1-H哪吒：

root@TinaLinux:/# ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
4--->8--->9--->10--->2--->7--->6--->5--->23--->11--->13--->12--->14--->15--->1--->29--->31--->30--->27--->28--->26--->25--->24--->20--->21--->22--->18--->3--->17--->19--->16
最优路径长度为:15402.341890
程序运行耗时:17.511801秒.
root@TinaLinux:/# ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
15--->1--->29--->31--->30--->27--->28--->26--->22--->21--->20--->25--->24--->19--->17--->18--->3--->16--->4--->2--->8--->9--->10--->7--->6--->5--->23--->11--->13--->12--->14
最优路径长度为:15593.696331
程序运行耗时:17.513332秒.
root@TinaLinux:/# ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
12--->14--->15--->1--->31--->30--->25--->20--->21--->22--->18--->3--->17--->19--->24--->26--->28--->27--->29--->11--->23--->16--->4--->8--->9--->10--->2--->5--->6--->7--->13
最优路径长度为:16155.269857
程序运行耗时:17.514657秒.

可以看到时间都在17s左右，哪吒稍快一点点。不过可惜手里没有类似的开发板对比，只能拿一个猎奇一点的来对比：

H3夸克（稚晖君那个小电脑）

由于使用的是H3，就直接用GCC编译即可生成执行文件。

发现屏幕没有中字模哈哈，串口运行看看：

pi@Quark-N:~/WorkSpace/SA_Algorithm$ ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
27--->30--->31--->1--->15--->14--->13--->12--->29--->11--->23--->5--->6--->7--->10--->9--->8--->2--->4--->16--->19--->17--->3--->18--->22--->21--->20--->24--->25--->26--->28
最优路径长度为:15683.072504
程序运行耗时:39.690700秒.
pi@Quark-N:~/WorkSpace/SA_Algorithm$ ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
27--->31--->30--->25--->20--->24--->23--->5--->6--->11--->29--->1--->15--->14--->12--->13--->7--->10--->9--->8--->2--->4--->16--->19--->17--->3--->18--->22--->21--->26--->28
最优路径长度为:16072.436112
程序运行耗时:39.947321秒.
pi@Quark-N:~/WorkSpace/SA_Algorithm$ ./test
采用模拟退火算法，初始温度T0=50000.00,降温系数q=0.98,每个温度迭代1000次,共降温1448次，得到的TSP最优路径为:
19--->16--->4--->8--->9--->10--->2--->7--->6--->5--->23--->24--->20--->25--->29--->11--->13--->12--->14--->15--->1--->31--->30--->27--->28--->26--->21--->22--->18--->3--->17
最优路径长度为:15996.839897
程序运行耗时:39.952181秒.

将近40秒。而且不出所料，执行完后非常烫手（毕竟板子尺寸摆在那里）。前两者相比起来就较为风轻云淡。当然了这之间其实也没什么可比性，毕竟夸克还同时点着个屏幕，玩起来纯属娱乐哈哈，如果有大佬有兴趣也可以尝试优化一下，我还是希望起个抛砖引玉的作用。

至于每次的结果为什么都不一样，简单按网上内容解释一下：SA算法本身是一种随机算法，转移向更差的解不是必然，而是概率性的，也就是说每次执行算法时，执行过程转移到的解可能都是完全不一样的。至于旅行商（Traveling Salesman Problem, TSP）问题，本身属于NP-hard问题，找不到存在多项式时间复杂度的解。

如果要求精确的解，目前可行的方法有枚举、分支限界、动态规划等，但这些方法适用的数据范围都很小，一旦数据规模变大，它们都将无能为力。所以目前广泛使用的大都是一些随机算法，比如蚁群、遗传等，模拟退火就是其中的一种，这些算法的一大特点就是通过随机去逼近最优解，但也有可能得到错解。

最后贴上一个经典视频：

ok，今天的帖就水到这里。

killer_p LV 3

@randolph 牛，虽然我看不懂但大为震惊